5.8 KiB
ECE 240: Electronic Circuits
Diodes
A diode is a two-terminal device that only allows current to flow in the direction of the arrow.
The current across a diode is, where \(I_s\) is a forced saturation current, \(V\) is the voltage drop across it, and \(V_T\) is the thermal voltage such that \(V_T=\frac{kT}{q}\), where \(T\) is the temperature, \(k\) is the Boltzmann constant, and \(q\) is the charge of an electron:
\[I=I_s\left(e^{V/V_T}-1\right)\]
!!! tip - \(V_T\approx\pu{25 mV}\) at 20°C - \(V_T\approx\pu{20 mV}\) at 25°C
A diode is open when current is flowing reverse the desired direction, resulting in zero current, until the voltage drop becomes so great that it reaches the breakdown voltage \(V_B\). Otherwise, the above current formula is followed.
Diodes are commonly used in rectifier circuits — circuits that convert AC to DC.
By preventing negative voltage, a relatively constant positive DC voltage is obtained. The slight dip between each hill is known as ripple \(\Delta V\).
In a simple series RC circuit, across a diode, Where \(R_LC>>\frac 1 \omega\), and \(f=\frac{\omega}{2\pi}\):
\[\Delta V\approx \frac{I_\text{load}}{2fC}\approx\frac{V_0}{2fR_LC}\]
Zener diodes
A Zener diode is a calibrated diode with a known breakdown voltage, \(V_B\). If the voltage across the diode would be greater than \(V_B\), it is capped at \(V_B\).
Voltage/current biasing
Solving for current for each element in a series returns a negative linear line and other non-linear lines.
- the linear line is the load line, which represents the possible solutions to the circuit when it is loaded
- Depending on the base current \(I_s\), the diode or transistor will be biased toward one of the curves, and the voltage and current will settle on one of the intersections, or bias points.
- To bias current, as \(R\to\infty\) (or, in practical terms, \(R>>diode\)), the slope of the load line \(\to 0\), which results in a constant current.
- To bias voltage, as \(R\to 0\), the slope of the load line \(\to\infty\), which results in a constant voltage.
The current across the resistor and the diode is the same:
\begin{align*}
i_D&=\frac{V_s}{R} \\
i_D&\approx I_se^{V_D/V_T}
\end{align*}If a diode is put in series with AC and DC voltage sources \(V_d(t)\) and \(V_D\):
\[\begin{align*} i_D(t)&=I_se^{(V_D+V_d(t))/V_T} \\ &=\underbrace{I_se^{V_D/V_T}}_\text{bias current}\ \underbrace{e^{V_d(t)/V_T}}_\text{$\approx 1+\frac{V_d}{V_T}$} \\ &=I_D\left(1+\frac{V_d}{V_T}\right) \\ &=\underbrace{I_D}_\text{large signal = bias = DC}+\underbrace{I_D\frac{V_d(t)}{V_T}}_\text{small signal = AC} \end{align*}\]
Diodes may act as resistors, depending on the bias current. They may exhibit a differential resistance: \[r_d=\left(\frac{\partial i_D}{\partial v_D}\right)^{-1} = \frac{V_T}{I_D}\]
!!! example Thus from the previous sequence:
$$i_D(t)=I_D+\frac{1}{r_d}V_d(t)$$Signal analysis
- Analyse DC signals
- assume blocking capacitors are open circuits
- turn off AC sources
- Analyse AC signals
- assume blocking capacitors are shorts
- turn off DC sources
- replace diode with effective resistor (the differential resistor)
!!! tip Most \(R\)s in the circuit can be assumed to be significantly greater than \(r_d\), so \(r_d\) can be removed in series or \(R\) can be removed in parallel.
!!! warning Oftentimes, turning off a DC source to nowhere is actually a short to ground.
MOSFETs
A MOSFET is a transistor. Current flows from the drain to the source, and only if voltage is applied to the gate.
In strictly DC, current passes the gate if the gate voltage is greater than the threshold voltage \(V_G>V_t\). The difference between the two is known as the overdrive voltage \(V_{ov}\):
\[V_{ov}=V_G-V_t\]
At a small \(V_{DS}\), or in AC, the slope of \(I_D\) to \(V_{DS}\) is proportional to \(V_G\). The channel transconductance \(g_{DS}\) represents this slope, which is constant based on the transconductance parameter of the device.
\[\frac{I_D}{V_{DS}}=g_{DS}=k_nV_{ov}\]
Before the saturation region, the current grows exponentially:
\[\boxed{I_s=k_n(V_{ov}-\tfrac 1 2V_{DS})V_{DS}}\]
Afterward, it remains constant, based on the overdrive voltage:
\[\boxed{I_s=\frac 1 2k_nV_{ov}^2}\]
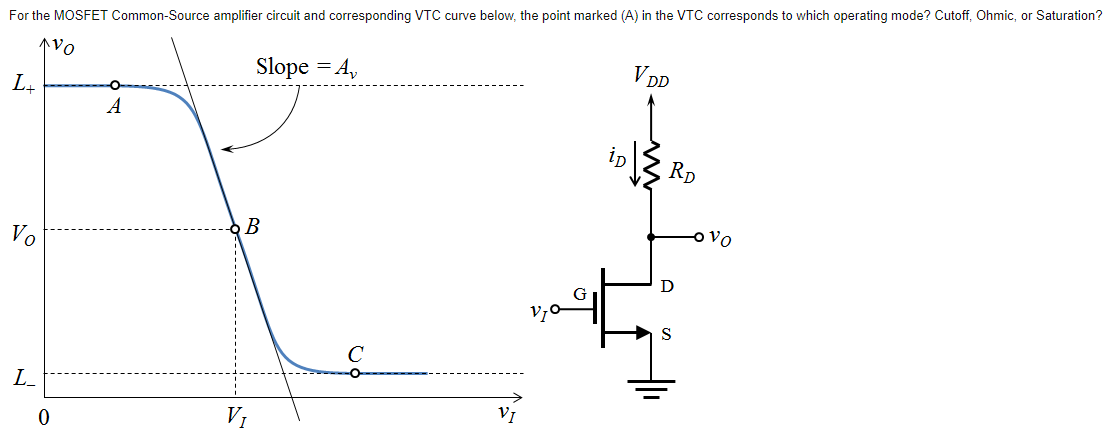
Common-source amplifiers
Where \(V_{out}=\)V_{DS}$:
\(|V_{ds}|>|V_{gs}|\) indicates AC voltage gain.
The gain can be modelled with Ohm’s law:
\[V_{DS}=V_{DD}-I_DR_D=V_{DD}-\frac 1 2k_n(V_{GS}-V_t)R_D\]
At a certain gate voltage:
\[\begin{align*} A_V&=\frac{\partial V_{DS}}{\partial V_{GS}} \\ &=-g_{DS}R_D \end{align*}\]