mirror of
https://gitlab.com/magicalsoup/Highschool.git
synced 2025-10-25 12:41:37 -04:00
10 KiB
10 KiB
Unit 4: Measurement and Geometry
Angle Theorems
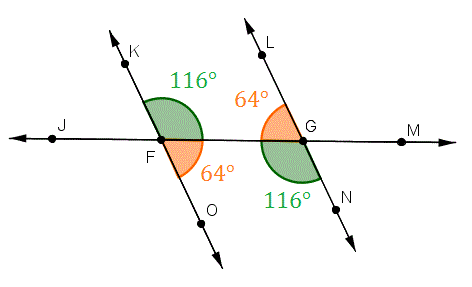
Transversal Parallel Line Theorems(TPT)- Alternate Angles are Equal
(Z-Pattern)
- Corresponding Angles Equal
(F-Pattern)
- Interior Angles add up to 180
(C-Pattern)
- Alternate Angles are Equal
Supplementary Angle Triangle(SAT)
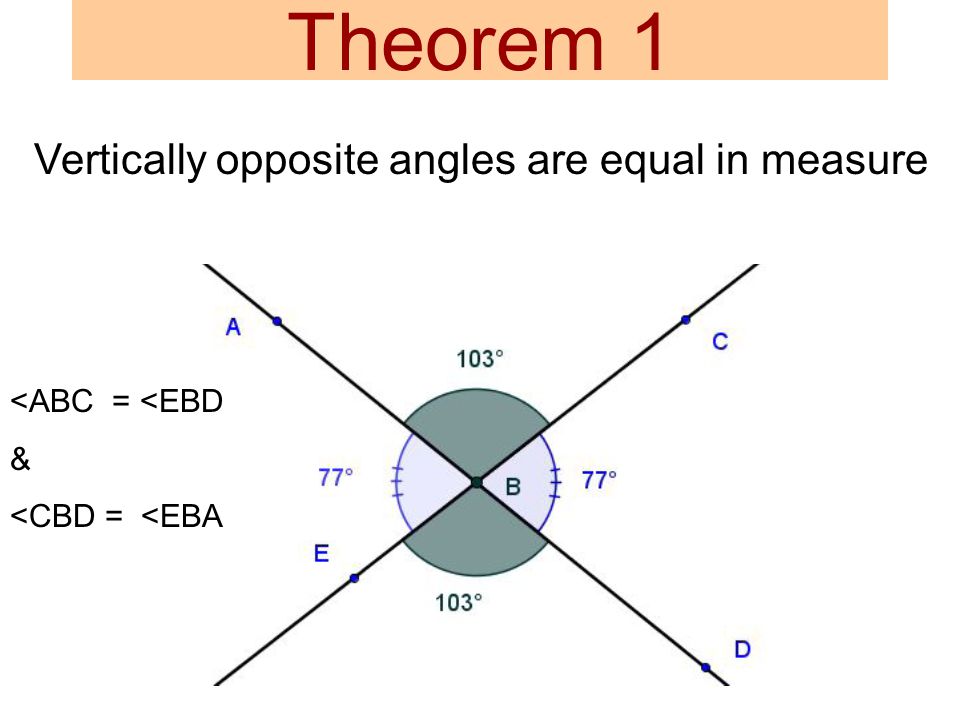
Opposite Angle Theorem (OAT)(OAT)
Complementary Angle Theorem(CAT)
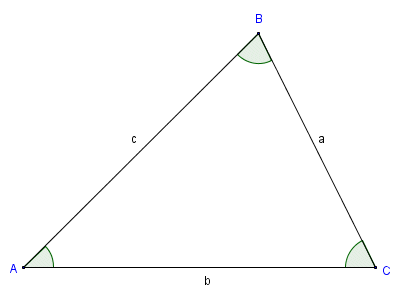
Angle Sum of a Triangle Theorem(ASTT)
Exterior Angle Theorem(EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
Isosceles Triangle Theorem(ITT)
Sum of The Interior Angle of a Polygon
The sum of the interioir angles of any polygon is
180(n-2)or180n - 360, wherenis the number of sides of the polygon
Exterior Angles of a Convex Polygon
Properties of Quadrilaterals
- Determine the shape using the properties of it
| Figure | Properties |
|---|---|
| Scalene Triangle | no sides equal |
| Isosceles Triangle | two sides equal |
| Equilateral Triangle | All sides equal |
| Right Angle Triangle | Two sides are perpendicular to each other |
| Parallelogram | Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other |
| Rectangle | Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length |
| Square | All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals |
| Rhombus | Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular |
| Trapezoid | There is one pair of opposite sides and they are parallel and unequal in length |
| Kite | The diagonals are perpendicular |
2D Geometry Equations
3D Geometry Equations
Optimization (For Maximimizing Area/Volume, or Minimizing Perimeter/Surface Area)
2D Objects
| Shape | Maximum Area | Minimum Perimeter |
|---|---|---|
| 4-sided rectangle | A rectangle must be a square to maximaze
the area for a given perimeter. The length is equal to the
width \(`A = lw`\) \(`A_{max} = (w)(w)`\) \(`A_{max} = w^2`\) |
A rectangle must be a square to minimaze
the perimeter for a given area. The length is equal to the
width. \(`P = 2(l+w)`\) \(`P_{min} = 2(w + w)`\) \(`P_{min} = 2(2w)`\) \(`P_{min} = 4w`\) |
| 3-sided rectangle | \(`l =
2w`\) \(`A = lw`\) \(`A_{max} = 2w(w)`\) \(`A_{max} = 2w^2`\) |
\(`l =
2w`\) \(`P = l+2w`\) \(`P_{min} = 2w+2w`\) \(`P_{min} = 4w`\) |
3D Objects
| 3D Object | Maximum Volumne | Minimum Surface Area |
|---|---|---|
| Cylinder(closed-top) | The cylinder must be similar to a cube
where \(`h = 2r`\) \(`V = πr^2h`\) \(`V_{max} = πr^2(2r)`\) \(`V_{max} = 2πr^3`\) |
The cylinder must be similar to a cube
where \(`h = 2r`\) \(`SA = 2πr^2+2πrh`\) \(`SA_{min} = 2πr^2+2πr(2r)`\) \(`SA_{min} = 2πr^2+4πr^2`\) \(`SA_{min} = 6πr^2`\) |
| Rectangular Prism(closed-top) | The prism must be a cube, where \(`l = w = h`\) \(`V = lwh`\) \(`V_{max} = (w)(w)(w)`\) \(`V_{max} = w^3`\) |
The prism must be a cube, where \(`l = w = h`\) \(`SA = 2lh+2lw+2wh`\) \(`SA_{min} = 2w^2+2w^2+2w^2`\) \(`SA_{min} = 6w^2`\) |
| Cylinder(open-top) | \(`h =
r`\) \(`V = πr^2h`\) \(`V_{max} = πr^2(r)`\) \(`V_{max} = πr^3`\) |
\(`h =
r`\) \(`SA = πr^2+2πrh`\) \(`SA_{min} = πr^2+2πr(r)`\) \(`SA_{min} = πr^2+2πr^2`\) \(`SA_{min} = 3πr^2`\) |
| Square-Based Rectangular Prism(open-top) | \(`h =
\frac{w}{2}`\) \(`V = lwh`\) \(`V_{max} = (w)(w)(\frac{w}{2})`\) \(`V_{max} = \frac{w^3}{2}`\) |
\(`h =
\frac{w}{2}`\) \(`SA = w^2+4wh`\) \(`SA_{min} = w^2+4w(\frac{w}{2})`\) \(`SA_{min} = w^2+2w^2`\) \(`SA_{min} = 3w^2`\) |
Labelling
Given any polygons, labelling the vertices must always:
- use
CAPITAL LETTERS - they have to be labeled in
clockwiseorcounter-clockwisedirections
- use
For a triangle, the side lengths are labeled in
LOWERCASE LETTERSassociated to the opposite side of the vertex
Median
Each median divides the triangle into 2 smaller triangles of equal area
The centroid is exactly \(`\dfrac{2}{3}`\)the way of each median from the vertex, or \(`\dfrac{1}{3}`\) the way from the midpoint of the opposite side, or
2:1ratio
The three medians divide the triangle into
6smaller triangles of equal area and3 pairsof congruent triangles
Terms:
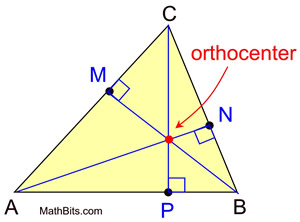
AltitudeThe height of a triangle, a line segment through a vertex and perpendicular to the opposite side
Orthocenter: where all 3 altitudes of the triangle intersectMidpoint: A point on a line where the length of either side of the point are equal
Median: A line segment joining the vertex to the midpoint of the opposite side
Midsegment: A line joining 2 midpoints of the 2 sides of a triangle
Centroid: The intersection of the 3 medians of a triangle
Proportionality theorem:
- The midsegment of a triangle is
halfthe length of the opposite side andparallelto the opposite side
- Three midsegment of a triangle divide
4 congruenttriangles with the same area
- The Ratio of the outer triangle to the triangle created by the 3
midsegments is
4 to 1
Tips
- Make sure to know your optimization formualas
- Read the word problems carefully, determine which formual to
use
- Never ASSUME, be sure to CALCULATE
as most of the time the drawings are NOT ACCURATE
- To find
missing area, take what you have, subtract what you don’t want
- Don’t be afraid to draw lines to help you solve the problem