4.5 KiB
Unit 6: System of Equations
Linear System
Two or more equation that you are working on all together at once on the same set of axes.
The lines may
crossorintersectat a point called thePoint of Intersection (POI).
The coordinated of the
POImust satisfy the equation of all the lines in a linear equation.In business, the
Point of Intersectionis known as the Break Even Point whereRevenue - Cost = Profit
when Profit = 0. There is no gain or loss.
Number of Solutions
Discriminant
The discriminant determines the number of solutions (roots) there are in a quadratic equation. \(`a, b , c`\) are the
coefficients and constant of a quadratic equation: \(`y = ax^2 + bx + c`\)
\(` D = b^2 - 4ac \begin{cases} \text{2 distinct real solutions}, & \text{if } D > 0 \\ \text{1 real solution}, & \text{if } D = 0 \\ \text{no real solutions}, & \text{if } D < 0 \end{cases} `\)
Solving Linear-Quadratic Systems
To find the point of intersection, do the following:
- Isolate both equations for \(`y`\)
- Set the equations equal to each other by
subsitutionEquation 1 = Equation 2 - Simplify and put everything on one side and equal to zero on the other side
- Factor
- Use zero-product property to solve for all possible x-values
- Subsitute the x-values to one of the original equations to solve for all y-values
- State a conclusion / the solution
There are 3 possible cases
In addition, to determine the number of solutions, you the Discriminant formula \(`D = b^2 - 4ac`\)
Ways to solve Systems of Equations
## 1. Subsitution
- Here we eliminate a variable by subbing in another variable from
another equation
- We usually do this method if a variable is easily isolated
- Example: - y = x + 10 (1) x + y + 34 = 40 (2) -
We can sub \(`(1)`\) into \(`(2)`\) to find \(`x`\), then you the value of \(`x`\) we found to solve for \(`y`\)
x + (x + 10) + 34 = 40 2x + 44 = 40 2x = -4 x = -2
- Then solve for \(`y`\)
y = -2 + 10 y = -8
## 2. Elimination - Here we eliminate a variable by basically
eliminate a variable from an equation
- We usually use this method first when the variables are not easily
isolated, then use subsitution to solve
- Example: - 2x + 3y = 10 (1) 4x + 3y = 14 (2) - We
can then use elimination
4x + 3y = 14 2x + 3y = 10 ------------ 2x + 0 = 4 x = 2
- Then sub the value of \(`x`\) into an
original equation and solve for \(`y`\)
2(2) + 3y = 10 3y = 6 y = 2
3. Graphing
- we can rewrite the equations into
y-intercept formand then graph the lines, and see where the lines intersect (P.O.I), and the P.O.I is the solution
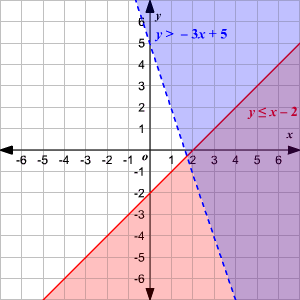
Solving Systems of Linear Inequalities
Find the intersection region as the
solution.
If
Use DashlineUse Solid lineShade the region abovethe line\(`y > mx + b`\) \(`y \ge mx + b`\) Shade the region belowthe line\(`y < mx + b`\) \(`y \le mx + b`\) If
\(`x > a`\)
\(`x \ge a`\)shade the region on the right
If
\(`x < a`\)
\(`x \le a`\)shade the region on the left
Step 1. change all inequalities to
y-intercept form
Step 2. graph the line
Step 3. shade the region where all the regions overlap
Tips
- Read the questions carefully and model the system of equations
correctly
- Be sure to name your equations
- Label your lines